Japanese version
I show you the instructions of Pop1 at the last session.
Pop1's program is fixed, this means we can not change the program. The Cybernetics coorp. considers their software is top secret matter. Even the people working for the company can not see it. Actually developers of the software can not read that. But, if you run the program, Pop1 displays what instruction is currently executed. So we can just write them down (Figure (I)). (The references (a), (b), (c) are in the last blog.) You may find that Pop1 has only three instructions.
Marvin``It's a waste to have three instructions in such a machine.''
Of course, we could construct a computer with one single instruction, which is Turing equivalent to the any computers we have. But, human needs understandings, Marvin. Please do not forget that. (There are several variations of one instruction set machine. My favorite one instruction computer is in the book, Computer Architecture: a Quantitative Approach.)
1 (a) Copy
2 (b) Delete head and tail
3 (a) Copy
4 (b) Delete head
5 (c) Add head
Figure (I) Pop1 program.
If you never wrote a computer program, you might wonder this is a real program or not. This is a real program. All the programs stuffs are composed of small program units (instructions), even the program of the weddings, TV program, Olympic game program, ... are the same way. Pop1 program is like this.
Figure (II) shows the all the procedures. I assume you can see the animation. But in case you can not see the animation or the procedure, I put the all figures also.
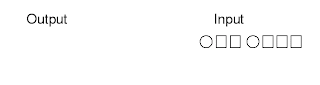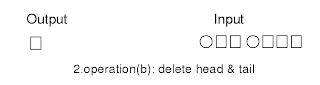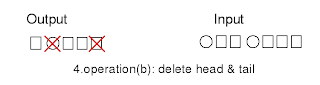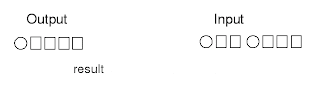Figure (II) Pop1 procedure (click on the image to see the animation gif)
Figure (1) Initial state
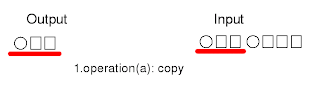Figure (2) 1. copy the input
Figure (3) 2. delete head and tail
Figure (4) 2. delete tail and head result
Figure (5) 3. copy the input
Figure (6) 4. delete head and tail
Figure (7) 4. delete head and tail result
Figure (8) 5. add head and tail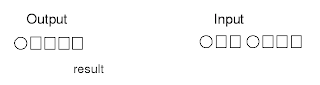
Figure (9) 5. add head and tail result
Now, what does this program? It does not matter the machine does something without meaning ``for human being,'' but I can show something meaning example here. Pop1 gets two inputs A and B, and then outputs one result C. Here A, B, and C are called variables. Maybe someone wonders what is variables? Let's talk about what is variable later if I remember it. I will write this as
Pop1(A, B) -> C.
Set A is 1, B is 2, then the result is
Pop1(1, 2) -> 3.
Pop1 gets input 1 and 2, then the result is 3. Let's see more.
Pop1(0, 0) -> 0
Pop1(0, 1) -> 1
Pop1(0, 2) -> 2
Pop1(1, 0) -> 1
Pop1(1, 1) -> 2
Pop1(1, 2) -> 3
Pop1(2, 0) -> 2
Pop1(2, 1) -> 3
Pop1(2, 2) -> 4
Can you see what is Pop1? This is ``Plus operation.'' Now you see why the machine's name is Pop1 (Plus OPeration 1). The name is for human. It actually does not matter if it is Lambda1, Machine1, Hokuspokus1, or whatever. (I followed the book from Sato and Sakurai.)
Let's rewrite this as in the usual notations.
Pop1(0, 0) -> 0 => 0 + 0 = 0
Pop1(0, 1) -> 1 => 0 + 1 = 1
Pop1(0, 2) -> 2 => 0 + 2 = 2
Pop1(1, 0) -> 1 => 1 + 0 = 1
Pop1(1, 1) -> 2 => 1 + 1 = 2
Pop1(1, 2) -> 3 => 1 + 2 = 3
Pop1(2, 0) -> 2 => 2 + 0 = 2
Pop1(2, 1) -> 3 => 2 + 1 = 3
Pop1(2, 2) -> 4 => 2 + 2 = 4
Finally, we have a computer, a machine that can compute in these days. At the old time, a computer is a person's job. I heard a lot of computer were women. Although this computer has ability to get angry if you mistake the inputs, it does not understand what the number is. It just follows a procedure. However, it ``looks like'' it can compute. This ``Looks like'' is important. I believe nowadays computer (2009) still does not understand what the number is. Computation is a machine procedure. It looks like computing, and the result is correct.
Appearance and contents, name and meaning are different things. But ``formalization'' is an idea if all the appearances are the same, let us think the contents are also the same. This is not a shallow idea. If there are perfect copies, you can not distinguish. Then they are the same. For example, you can buy a software, but each software is a copy. We expect all the software have the same functionality. This is important from the industrial point of view. Of course, exact I am not ready to accept the exact copy of myself -- a copy of human being. But, if I buy two same model computers, I want to have the same. If I buy the same DVD title, I want to have the same. Also I expect the quality should not matter if I bought it from a shop in Berlin or in Frankfurt.
On the other hand, I prefer a hand written mail from my friends since each of them is different. I look for the eternal truth in mathematics, but I love also a limited life. It looks like contradiction. How is the opinion of Marvin, who experienced the universe five times.
I show you the instructions of Pop1 at the last session.
Pop1's program is fixed, this means we can not change the program. The Cybernetics coorp. considers their software is top secret matter. Even the people working for the company can not see it. Actually developers of the software can not read that. But, if you run the program, Pop1 displays what instruction is currently executed. So we can just write them down (Figure (I)). (The references (a), (b), (c) are in the last blog.) You may find that Pop1 has only three instructions.
Marvin``It's a waste to have three instructions in such a machine.''
Of course, we could construct a computer with one single instruction, which is Turing equivalent to the any computers we have. But, human needs understandings, Marvin. Please do not forget that. (There are several variations of one instruction set machine. My favorite one instruction computer is in the book, Computer Architecture: a Quantitative Approach.)
1 (a) Copy
2 (b) Delete head and tail
3 (a) Copy
4 (b) Delete head
5 (c) Add head
Figure (I) Pop1 program.
If you never wrote a computer program, you might wonder this is a real program or not. This is a real program. All the programs stuffs are composed of small program units (instructions), even the program of the weddings, TV program, Olympic game program, ... are the same way. Pop1 program is like this.
Figure (II) shows the all the procedures. I assume you can see the animation. But in case you can not see the animation or the procedure, I put the all figures also.
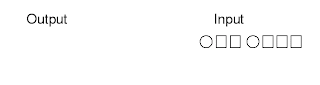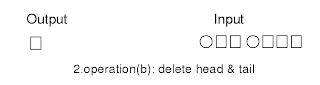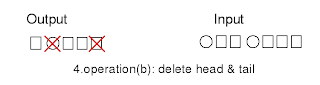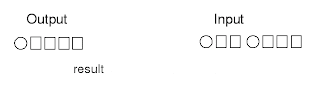Figure (II) Pop1 procedure (click on the image to see the animation gif)
Figure (1) Initial state
Figure (2) 1. copy the input
Figure (3) 2. delete head and tail
Figure (4) 2. delete tail and head result
Figure (5) 3. copy the input
Figure (6) 4. delete head and tail
Figure (7) 4. delete head and tail result
Figure (8) 5. add head and tail
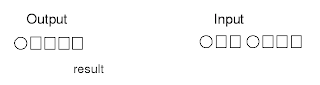Figure (9) 5. add head and tail resultNow, what does this program? It does not matter the machine does something without meaning ``for human being,'' but I can show something meaning example here. Pop1 gets two inputs A and B, and then outputs one result C. Here A, B, and C are called variables. Maybe someone wonders what is variables? Let's talk about what is variable later if I remember it. I will write this as
Pop1(A, B) -> C.
Set A is 1, B is 2, then the result is
Pop1(1, 2) -> 3.
Pop1 gets input 1 and 2, then the result is 3. Let's see more.
Pop1(0, 0) -> 0
Pop1(0, 1) -> 1
Pop1(0, 2) -> 2
Pop1(1, 0) -> 1
Pop1(1, 1) -> 2
Pop1(1, 2) -> 3
Pop1(2, 0) -> 2
Pop1(2, 1) -> 3
Pop1(2, 2) -> 4
Can you see what is Pop1? This is ``Plus operation.'' Now you see why the machine's name is Pop1 (Plus OPeration 1). The name is for human. It actually does not matter if it is Lambda1, Machine1, Hokuspokus1, or whatever. (I followed the book from Sato and Sakurai.)
Let's rewrite this as in the usual notations.
Pop1(0, 0) -> 0 => 0 + 0 = 0
Pop1(0, 1) -> 1 => 0 + 1 = 1
Pop1(0, 2) -> 2 => 0 + 2 = 2
Pop1(1, 0) -> 1 => 1 + 0 = 1
Pop1(1, 1) -> 2 => 1 + 1 = 2
Pop1(1, 2) -> 3 => 1 + 2 = 3
Pop1(2, 0) -> 2 => 2 + 0 = 2
Pop1(2, 1) -> 3 => 2 + 1 = 3
Pop1(2, 2) -> 4 => 2 + 2 = 4
Finally, we have a computer, a machine that can compute in these days. At the old time, a computer is a person's job. I heard a lot of computer were women. Although this computer has ability to get angry if you mistake the inputs, it does not understand what the number is. It just follows a procedure. However, it ``looks like'' it can compute. This ``Looks like'' is important. I believe nowadays computer (2009) still does not understand what the number is. Computation is a machine procedure. It looks like computing, and the result is correct.
Appearance and contents, name and meaning are different things. But ``formalization'' is an idea if all the appearances are the same, let us think the contents are also the same. This is not a shallow idea. If there are perfect copies, you can not distinguish. Then they are the same. For example, you can buy a software, but each software is a copy. We expect all the software have the same functionality. This is important from the industrial point of view. Of course, exact I am not ready to accept the exact copy of myself -- a copy of human being. But, if I buy two same model computers, I want to have the same. If I buy the same DVD title, I want to have the same. Also I expect the quality should not matter if I bought it from a shop in Berlin or in Frankfurt.
On the other hand, I prefer a hand written mail from my friends since each of them is different. I look for the eternal truth in mathematics, but I love also a limited life. It looks like contradiction. How is the opinion of Marvin, who experienced the universe five times.
Comments